In the world of mechanics and material science, understanding strain is very important. It tells us how much a material changes shape or length when a force is applied. This article will explain what is strain, its meaning, and definition in simple terms. We’ll also cover the strain formula, the correct strain symbol, and the basic strain equation used in calculations. Additionally, you will learn the types of strain found in mechanics, the difference between stress vs strain, and a step-by-step guide on how to calculate strain. Whether you’re a student or just curious about physics, this guide will help you understand everything you need to know about strain in a clear and easy way.
What is Strain?
Strain is a fundamental concept in mechanics and materials science that describes how materials deform when forces are applied to them. When an external force acts on a solid object, it can cause the object to change its shape or size. This deformation is called strain. Specifically, strain measures the amount of deformation relative to the original dimensions of the material.
There are different types of strain depending on how the material changes shape. The most common type is normal strain, which occurs when an object stretches or compresses along a single axis. For example, if you pull on a metal rod, it elongates, causing tensile strain. Conversely, if you compress it, the rod shortens, producing compressive strain. Another important type is shear strain, which measures how an object changes shape by sliding layers over one another, like when you twist a rubber band.
Strain is expressed as a ratio of the change in length (or displacement) to the original length. This ratio is dimensionless, meaning it has no units, and it can also be written as a percentage. For example, a strain of 0.01 means the material has stretched by 1% of its original length.
Understanding strain is essential because it helps engineers and scientists predict how materials will behave under loads, ensuring that structures such as bridges, buildings, and machinery parts remain safe and functional. Excessive strain can lead to permanent deformation or even failure, so measuring strain allows for better design and material selection.
Strain Meaning:
Strain is a measure of deformation representing the displacement between particles in a material body relative to a reference length. It indicates how much an object stretches, compresses, or changes shape when subjected to external forces. Strain is a dimensionless quantity, often expressed as a ratio or percentage, and helps engineers and scientists understand how materials behave under stress to prevent failure or damage.
Strain Definition:
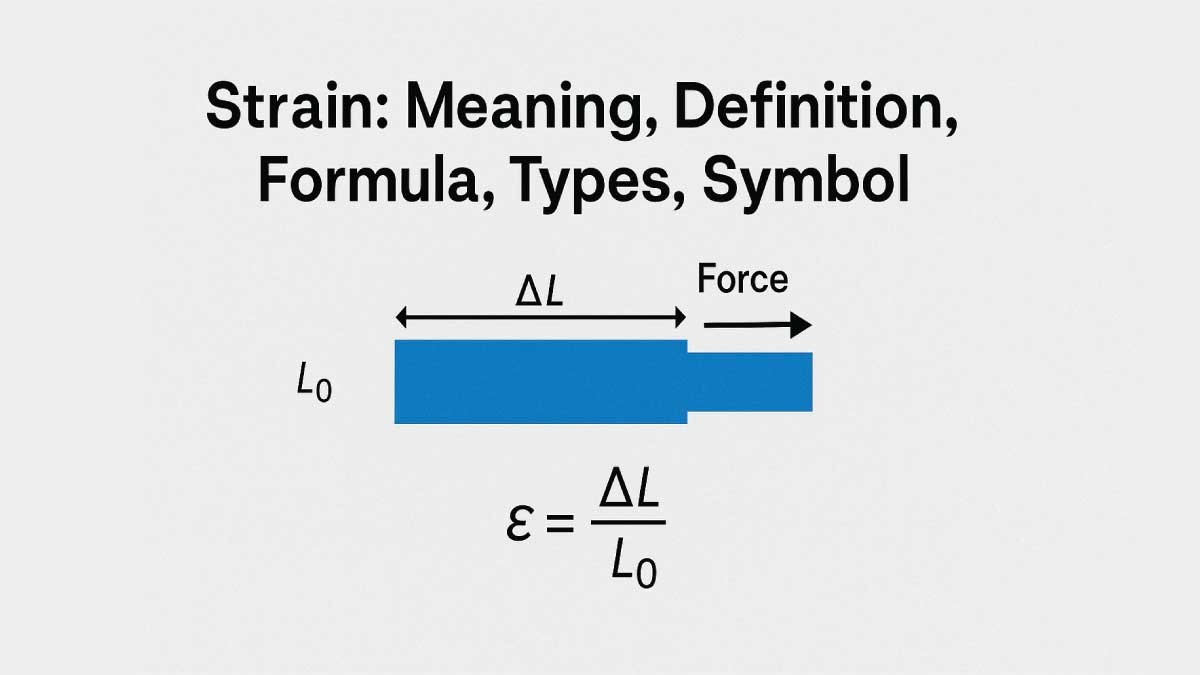
Strain is defined as the ratio of change in length to the original length of a material when it experiences deformation due to applied forces. It quantifies the extent to which a material elongates, compresses, or distorts. Mathematically, strain (ε) is given by ε = ΔL / L₀, where ΔL is the change in length and L₀ is the original length. It is a dimensionless value and can be expressed as a decimal or percentage. Strain helps in analyzing material behavior in fields like mechanical engineering, materials science, and structural analysis to ensure safety and reliability.
Also Read:
Strain Formula:
Strain is calculated as the ratio of the change in length to the original length of a material when it deforms under applied force. The basic formula for normal strain (ε) is:
ε=ΔLL0\varepsilon = \frac{\Delta L}{L_0}
where:
ε\varepsilon (epsilon) = strain (dimensionless),
ΔL\Delta L = change in length (final length minus original length),
L0L_0 = original length.
If the material elongates, the strain is positive (tensile strain), and if it compresses, the strain is negative (compressive strain).
For shear strain, the formula is different and relates to angular deformation, but the above formula is the most commonly used for linear or normal strain. Strain is a dimensionless quantity often expressed as a decimal or percentage.
Strain Symbol:
The symbol for strain is typically the Greek letter ε (epsilon), which represents normal or linear strain. This strain measures the relative change in length of a material when subjected to tensile or compressive forces. It is a dimensionless quantity calculated as the ratio of the change in length to the original length. For shear strain, which describes angular deformation, the symbol γ (gamma) is used instead. Both ε and γ help engineers and scientists quantify deformation in materials under different types of stress, allowing accurate analysis of material behavior and structural integrity.
Also Read:
Strain Equation:
The strain equation defines how much a material deforms under stress. The most common strain equation is for normal (linear) strain, expressed as:
ε=ΔLL0\varepsilon = \frac{\Delta L}{L_0}
where ε\varepsilon is the strain (dimensionless), ΔL\Delta L is the change in length, and L0L_0 is the original length of the material. This equation calculates the relative elongation or compression of an object. For shear strain, the equation is different, typically expressed as the angular displacement between layers, denoted by γ\gamma. These equations are fundamental in material science and engineering for analyzing deformation.
Stress vs. Strain:
Stress and strain are fundamental concepts in materials science and mechanical engineering that describe how materials respond to forces.
Stress is the internal force per unit area within a material that arises when external forces act on it. It measures how much load a material experiences over a specific cross-sectional area. The formula for stress (σ\sigma) is:
σ=FA\sigma = \frac{F}{A}
where FF is the applied force and AA is the cross-sectional area. Stress is measured in units such as pascals (Pa) or pounds per square inch (psi). It describes the intensity of internal forces trying to resist deformation.
On the other hand, strain measures the material’s deformation or change in shape/size caused by the applied stress. It is the ratio of change in length to the original length, representing how much a material stretches or compresses under stress. Strain is dimensionless and calculated by:
ε=ΔLL0\varepsilon = \frac{\Delta L}{L_0}
where ΔL\Delta L is the change in length and L0L_0 is the original length.
The relationship between stress and strain is critical for understanding material behavior. In the elastic region, they are proportional, as described by Hooke’s Law:
σ=Eε\sigma = E \varepsilon
where EE is the modulus of elasticity or Young’s modulus, a measure of material stiffness.
In summary, stress is the cause (force per area), and strain is the effect (deformation) of that force on a material. Understanding both helps engineers design safe and efficient structures.
Also Read:
Types of Strain in Mechanics:
In mechanics and materials science, strain refers to the deformation or change in shape and size of a material when subjected to external forces or loads. Different types of strain describe the way materials deform depending on the nature and direction of applied forces. Understanding these types is essential for engineers to analyze structural behavior and prevent failure. The main types of strain include normal strain, shear strain, and volumetric strain.
1. Normal Strain (Axial Strain)
Normal strain occurs when an object experiences elongation or compression along a single axis due to tensile or compressive forces. It measures the relative change in length compared to the original length. Normal strain can be:
Tensile strain: When the material is stretched, increasing its length.
Compressive strain: When the material is compressed, decreasing its length.
The formula for normal strain ε\varepsilon is:
ε=ΔLL0\varepsilon = \frac{\Delta L}{L_0}
where ΔL\Delta L is the change in length, and L0L_0 is the original length.
Normal strain is dimensionless and usually expressed as a decimal or percentage. For example, a strain of 0.005 means the material has stretched 0.5% of its original length.
2. Shear Strain
Shear strain measures the deformation of a material due to forces applied parallel or tangential to its surface, causing layers of the material to slide relative to each other. Instead of changing length, shear strain causes angular distortion.
The symbol for shear strain is γ\gamma, and it is defined as the angular displacement in radians between two originally perpendicular lines. Shear strain is given by:
γ=tanθ≈θ\gamma = \tan \theta \approx \theta
where θ\theta is the small angle (in radians) formed by the distortion.
This strain type is common in materials subjected to torsion or twisting forces. For example, when you twist a rubber band, it experiences shear strain.
Also Read:
3. Volumetric Strain (Dilatation)
Volumetric strain refers to the change in volume of a material due to uniform pressure or stress applied in all directions. It is the ratio of the change in volume ΔV\Delta V to the original volume V0V_0:
εv=ΔVV0\ varepsilon_ v = \frac{\Delta V}{V_0}
Volumetric strain can result from compressive or tensile stresses that cause the material to expand or contract uniformly. This type is important in fields like geotechnical engineering, where soil or rock volume changes under load must be considered.
4. Other Types of Strain
Engineering strain vs. true strain: Engineering strain assumes deformation is uniform and calculated using the original length. True strain accounts for continuous deformation and is more accurate for large strains.
Plastic strain: Permanent deformation after the load is removed.
Elastic strain: Temporary deformation that disappears when the load is removed.
Also Read:
How to Calculate Strain:
Strain is a measure of how much a material deforms under an applied force. It quantifies the relative change in dimension, such as length or shape, compared to the material’s original size. Calculating strain helps engineers and scientists understand material behavior and ensure structural safety.
Step 1: Identify the Original Length (L0L_0)
First, you need the original length of the object or material before any force is applied. This is usually measured in meters (m), millimeters (mm), or inches (in).
Step 2: Measure the Change in Length (ΔL\Delta L)
Next, measure the length of the material after deformation. The change in length is the difference between the new length (LL) and the original length:
ΔL=L−L0\Delta L = L – L_0
If the material has stretched, ΔL\Delta L is positive. If compressed, ΔL\Delta L is negative.
Step 3: Apply the Strain Formula
The most common type of strain is normal strain, which is calculated as:
ε=ΔLL0\varepsilon = \frac{\Delta L}{L_0}
where:
ε\varepsilon (epsilon) is the strain (dimensionless),
ΔL\Delta L is the change in length,
L0L_0 is the original length.
This ratio gives the relative deformation. Since strain is dimensionless, it can be expressed as a decimal or multiplied by 100 to get a percentage.
Also Read:
Example:
Suppose a steel rod originally 2 meters long stretches to 2.002 meters when pulled.
L0=2.0 mL_0 = 2.0 \, m
L=2.002 mL = 2.002 \, m
ΔL=2.002−2.0=0.002 m\Delta L = 2.002 – 2.0 = 0.002 \, m
Calculate strain:
ε=0.0022.0=0.001\varepsilon = \frac{0.002}{2.0} = 0.001
This means the rod has stretched by 0.1%.
Additional Notes
For shear strain, calculation involves measuring angular displacement, not length.
For large deformations, true strain formulas are used, which consider continuous change.
By following these steps, you can accurately calculate strain and analyze material deformation.
Also Read:
A Complete Guide to Torque: Definition, Formula, Units, and More
Conclusion:
To sum up, strain is a key concept in mechanics that helps us understand how materials behave under force. By knowing the strain meaning and strain definition, we can better predict how objects stretch, compress, or deform. Using the strain formula and strain equation, you can easily calculate how much a material changes. It’s also important to recognize the correct strain symbol and understand the various types of strain such as normal and shear. Finally, comparing stress vs strain helps explain how force causes deformation. By learning how to calculate strain, you gain useful knowledge for solving real-world engineering and physics problems.
Also Read:
FAQs:
What is strain in simple words?
Strain is the amount a material stretches, compresses, or changes shape when a force is applied to it. It shows how much the object deforms compared to its original size. Strain has no unit because it’s a ratio. It’s used in physics and engineering to understand how materials behave under stress and helps prevent structural damage or failure.
What is the difference between stress and strain?
Stress is the force applied per unit area, while strain is the deformation or change caused by that force. Stress has units (like pascals), but strain is dimensionless. Stress is the cause, and strain is the effect. Engineers use both to study material strength, elasticity, and failure under loads. Understanding this difference is key in designing safe and efficient structures.
How do you calculate strain?
Strain is calculated using the formula:
Strain=Change in Length Original Length\text{Strain} = \frac{\text{Change in Length}}{\text{Original Length}}
It’s a ratio that shows how much a material has deformed. For example, if a rod stretches 2 mm and was originally 200 mm long, the strain is 0.01 (or 1%). Strain has no units and can be expressed as a decimal or percentage.
What are the types of strain in mechanics?
The main types of strain are normal strain, shear strain, and volumetric strain. Normal strain occurs when an object stretches or compresses along its length. Shear strain happens when layers slide over each other, changing shape without changing volume. Volumetric strain refers to a change in the material’s overall volume. Each type helps engineers understand different types of deformation under force.
What is the symbol for strain?
The standard symbol for normal strain is the Greek letter ε (epsilon). It represents the ratio of change in length to original length. For shear strain, the symbol used is γ (gamma). These symbols are commonly used in engineering formulas and stress-strain diagrams to calculate how materials deform under load.
What is the formula for strain in physics?
The basic formula for normal strain is:
ε=ΔLL0\varepsilon = \frac{\Delta L}{L_0}
Where ε\varepsilon is the strain, ΔL\Delta L is the change in length, and L0L_0 is the original length. This formula calculates the amount of deformation in a material due to applied force. It’s widely used in physics and mechanical engineering to analyze structural behavior.
Can strain be negative?
Yes, strain can be negative when a material is compressed instead of stretched. A negative strain means the object is shortening due to applied force. This is called compressive strain, as opposed to tensile strain, which is positive and occurs when the material is stretched. Both values are important for understanding how materials respond under different types of loads.